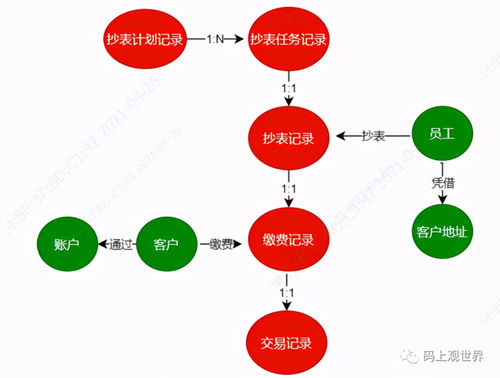
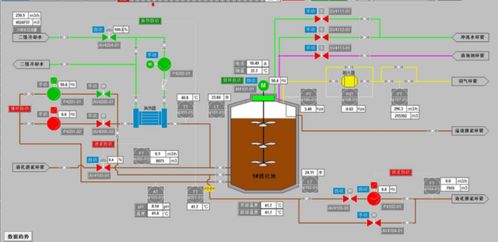
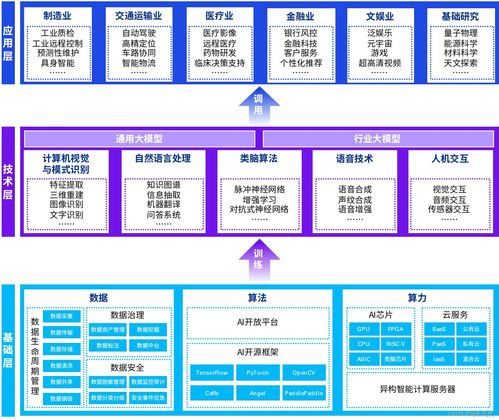
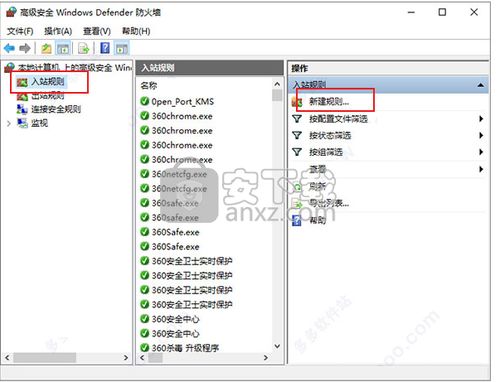
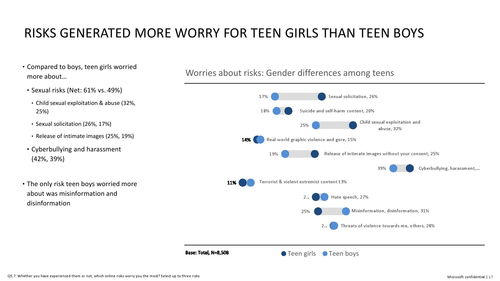
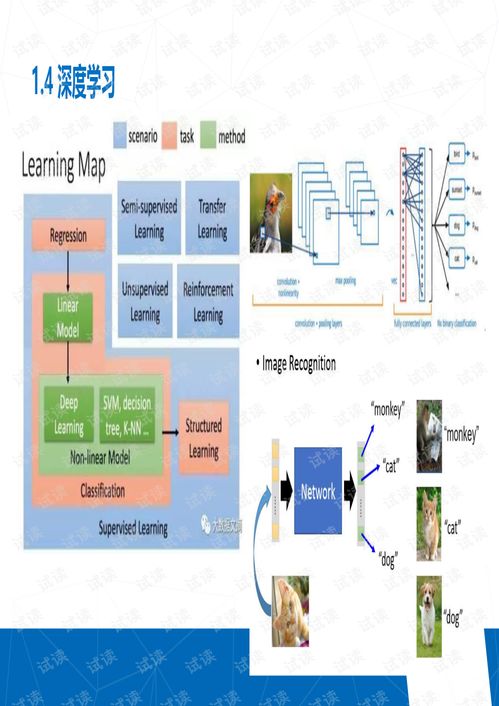
人工智能教程 數(shù)學(xué)基礎(chǔ)課程1.1 數(shù)學(xué)分析v2 實(shí)數(shù)的連續(xù)性和完備性
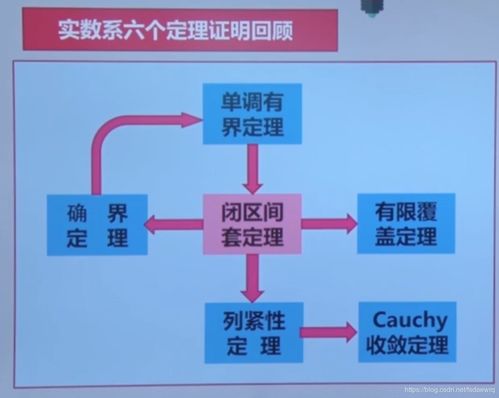
在人工智能的基礎(chǔ)軟件開發(fā)中,數(shù)學(xué)分析扮演著至關(guān)重要的角色。本課程是數(shù)學(xué)基礎(chǔ)課程的第一部分,聚焦于實(shí)數(shù)的連續(xù)性和完備性,這兩個(gè)概念為理解數(shù)據(jù)處理的連續(xù)性、優(yōu)化算法的收斂性以及機(jī)器學(xué)習(xí)模型的穩(wěn)定性奠定了理論基礎(chǔ)。
一、實(shí)數(shù)的連續(xù)性
實(shí)數(shù)的連續(xù)性是指實(shí)數(shù)軸上的點(diǎn)沒有“間隙”,任何兩個(gè)不同的實(shí)數(shù)之間都存在無限多個(gè)其他實(shí)數(shù)。這一性質(zhì)源于實(shí)數(shù)的基本性質(zhì),例如,任意有上界的非空實(shí)數(shù)集必有上確界。連續(xù)性在人工智能中至關(guān)重要,因?yàn)樗_保了函數(shù)的連續(xù)性分析,這在梯度下降等優(yōu)化算法中被廣泛應(yīng)用。例如,在訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí),我們經(jīng)常處理連續(xù)損失函數(shù),其導(dǎo)數(shù)依賴于實(shí)數(shù)的連續(xù)性以找到最小值點(diǎn)。
二、實(shí)數(shù)的完備性
實(shí)數(shù)的完備性意味著實(shí)數(shù)集是“完整”的,即任何柯西序列(一種逐漸趨近的序列)在實(shí)數(shù)集中都有極限點(diǎn)。這一定義源于實(shí)數(shù)系統(tǒng)的構(gòu)造,例如戴德金分割或康托爾公理。在人工智能基礎(chǔ)軟件開發(fā)中,完備性保證了算法的收斂性。例如,在機(jī)器學(xué)習(xí)中,許多迭代算法(如隨機(jī)梯度下降)依賴于實(shí)數(shù)空間的完備性來確保模型參數(shù)最終收斂到最優(yōu)解,避免了因數(shù)值不完整導(dǎo)致的發(fā)散問題。
三、實(shí)際應(yīng)用與總結(jié)
實(shí)數(shù)的連續(xù)性和完備性共同支撐了人工智能軟件的開發(fā)。在數(shù)據(jù)處理中,連續(xù)性允許我們對傳感器數(shù)據(jù)進(jìn)行平滑處理;在算法設(shè)計(jì)中,完備性確保優(yōu)化過程穩(wěn)定。理解這些概念有助于開發(fā)者設(shè)計(jì)更高效的AI系統(tǒng),避免數(shù)值錯(cuò)誤。本課程旨在強(qiáng)化數(shù)學(xué)基礎(chǔ),為后續(xù)深入學(xué)習(xí)人工智能算法打下堅(jiān)實(shí)基礎(chǔ)。繼續(xù)學(xué)習(xí)下一節(jié),我們將探討函數(shù)的極限與連續(xù)性。
如若轉(zhuǎn)載,請注明出處:http://www.380hy.com/product/10.html
更新時(shí)間:2026-02-14 20:09:07